Preface

When we say that a model is a black box, we don't mean its internal operations remain a mystery, but the fact that we are unable to understand these operations and why they work. Suppose we train a model to predict voltage with current, we design a linear model \( y = Ax + b \). To model the system's behavior, we use a dataset containing the voltage values when different current, and we will get an appropriate weight scaler \( A \) after training the model with optimization algorithms. Now what does this equation \( y = Ax + b \) mean? The variables \( x, y \) simply represent the input current and voltage value, while scaler \( A \) measures the impact on voltage as the current is going through the system, and \( b \) might be just an error or bias (when the system is not linear). In that case, we know exactly what these variables represent, and it is easy for us to predict the model's behavior (like what happens to \( y \) when we raise \( x \)) and explain why this is happening (the impact on \( y \) remains linear to the change of \( x \)).

However, what happens when \( x \) is an image and \( y \) has another meaning? Suppose we have a dataset that records how people evaluate paintings, and surely we can get an \( A \) after training, but what does \( A \) mean in this case? Is it proper? If the \( A \) value is not proper, how can we modify our model to promote its performance? All of these remain unknown. It is the same linear model and we just change the meaning of the input and output, and the degree to which we can interpret this model has changed wildly.

In general, interpretability refers to the degree to which humans understand the internal mechanism of a model, and the reasons behind its outputs. In the early stage of the development of deep learning, people seldom need to interpret the mechanism behind models, and what they expect was to make models perform better on the given datasets. However, things start to change as deep models are applied to critical fields such as assisting medical treatment, making financial investments or legal judgements, and even occasions involving military uses. People nowadays want models to be interpretable mainly due to the following reasons:

1. We don't trust the outputs of a model unless we now exactly how they are produced.
2. It's hard to design, debug or simplify a model because there are no bases at all.
3. Models might encounter moral problems such as data bias.

Zhang et al. in their survey defined six research directions in the field of model interpretability , which are outlined as follows:

1. Visualization of intermediate layers. This approach is generally the most direct one, and methods such as including gradient-based interpretability belong to this type.
2. Diagnosis of representation. Sometimes we wonder what the model knows, and how that information is encoded inside its layers. The main idea behind this technique is to find the hidden rules behind weights and activations.
3. Disentanglement of patters from complex structures. This approach assumes that the input information consists of separable parts that are interpretable by humans.
4. Explainable models. By bulding models that are self-explanatory, we don't need to interpret exsisting models that are not interpretable.
5. Human-computer interaction. This method requires the model to be able to interact with its human users, and yield the necessary, interpretable information for its users.

Except the above, Zhang et al. also demenstrated the importance of interpretability metrics (which is the sixth direction), providing the way to judge whether or not, and to what extent can we consider a model to be interpretable. Such metrics are unlike traditional performance index such as accuracy and inference speed, since they can't be well-defined in every case. But generally, a good explanation of how a model works should be faithful to the true mechanism inside the model. Explanations can be plausible to humans because they are what humans want to see, but unfaithful to the model. Such problems encourage us to discover an objective, or better a quantitative metric to evaluate how interpretable models are.

In the following sections, we walk through the most important discoveries in the field of interpretability and its related fields. We begin with some commonly used concepts and utilities.

Concept

Sometimes, models with simple structures can have so-called internal interpretability. Such models are well-defined and humans can directly tell what makes the model generate such outputs. A typical internally interpretable model is the linear regression model, whose output is defined by \[ y = \sum_{i = 1}^n \alpha_i x_i. \] Given a series of inputs \( \{x_i\}_{i = 1}^n \), when a coefficient \( \alpha_j \) is large, the output \( y \) is also likely to be large. This implies that the \( j \)-th input can significantly affect the output. To explain an output, we only need to look at the coefficients, which directly display their importance to the final result. Models like a linear regression model are interpretable due to their structures (like the interpretable coefficients in linear regression models), and are therefore internally interpretable. They can be also considered to be white boxes, compared to deep neural networks which are generally black boxes.

What happens if a model is not internally explainable? Some models are still considered to be interpretable if we can provide a post-hoc explanation. For example, consider a pre-trained classification CNN. It produces an output by letting the input information through its structures, yielding feature maps in each of its layers. By visualizing the output of these feature maps, we might be able to see what matters the most in each layer (if we can interpret them). Post-hoc interpretability sometimes require an explanatory model designed for each single model, and can be therefore hard to realize.

Latest Achievements

This section outlines several latest achievements in the field of interpretablility, from today's well-known LLM to strcutures that are more abstract and complicated. We begin with chain-of-thought prompting, which has now been widely used in LLMs developed by large AI companies such as OpenAI and Google.

Chain-of-Thought

Proposed by developers at Google in 2022 , chain-of-thought (CoT) has become a representative way of showing human-interpretable reasoning logic in large language models. Basically, the idea behind this technique is to split the process of generating answers directly into a few logical fragments that are often expressed by texts, and in each fragment the model generates an interpretable intermediate conclusion, sequentially leading to the final answer. Users may interpret the reasoning process by looking into each of the fragments, and determine whether the final answer is reliable.

To implement CoT, the authors proposed that users may use a CoT-styled prompting. This prompting style has few-shot and one-shot variants. For one-shot CoT, the user typically includes a trigger such as "Let's think step by step" in the prompt, and the model might produce a step-by-step analysis accordingly. For few-shot CoT, the prompt includes two similar problems. The second problem is the one the user really wants to ask, while the first problem is a similar problem to the second, with a step-by-step answer. By providing the first problem and its step-by-step anwser as an example, the model might mimic its logic and produce answers of the same logical framework. The following figure shows an example of few-shot CoT prompting.

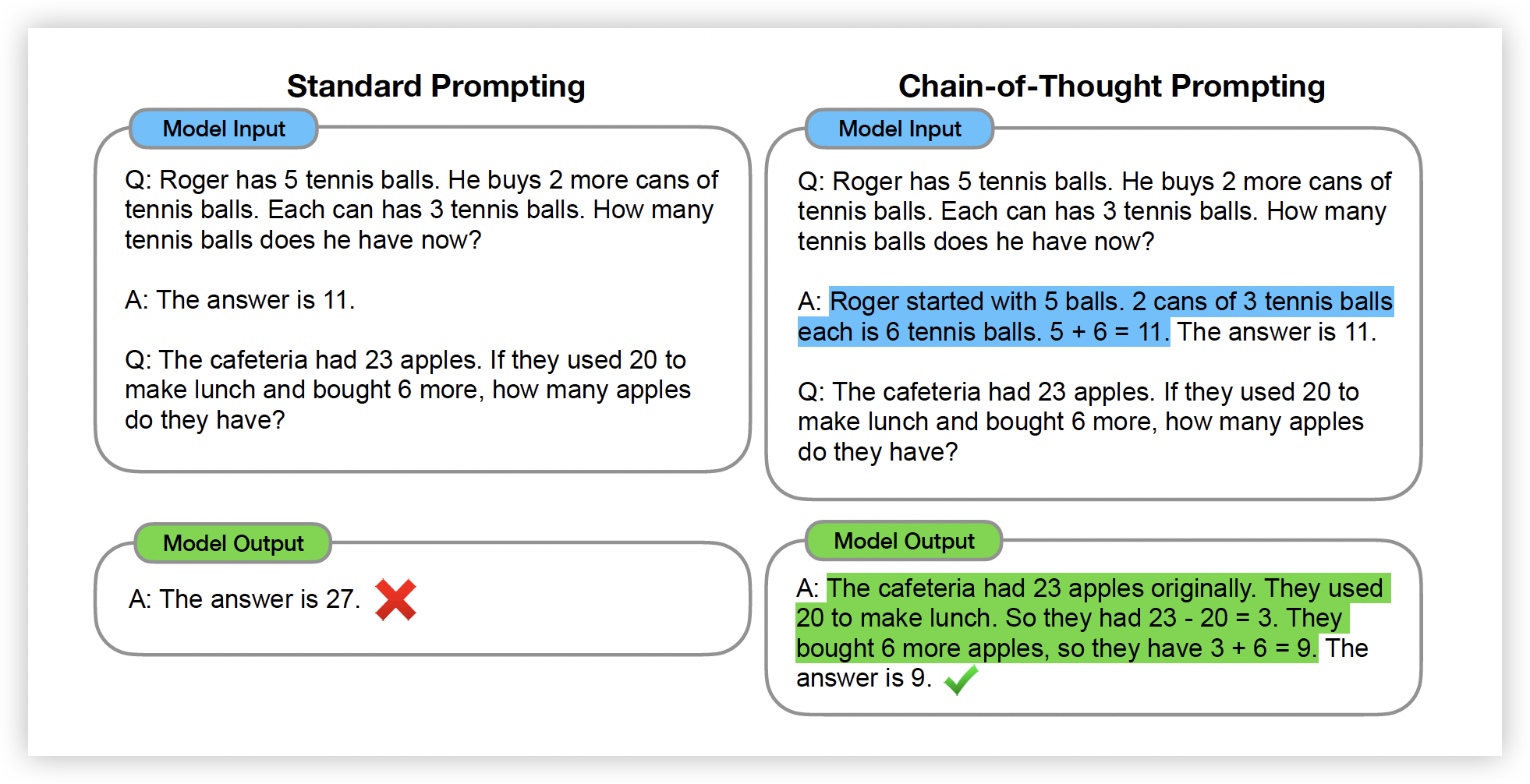
Few-Shot CoT Prompting (Jason Wei et al. )

Empirical evidence shown in suggests that CoT prompting leads to significantly more satisfying answers. But after all, CoT prompting is required on the user-side, which does not provide much guidance to the design of LLM using a CoT-styled reasoning. However, CoT as a strategy of design has been guiding LLM developers to explore the model-side CoT, that is, the model automatically splits its answers into fragments without explicit user prompt. This techinique has been universally used in today's popular LLMs such as ChatGPT 4o series.

Self-Consistency

An interesting variant of CoT is the self-consistent CoT, which is proposed by Xuezhi Wang et al. and published in 2023 . This approach mimics the reasoning logic of humans: for a fixed problem, we may adopt different reasoning and reach the same result (known as consistency). If the results are different, we simply choose the one we are most confident about. Similarly, we feed the LLM with a well-written CoT prompt multiple times, forming a set of outputs. Each output consists of its reasoning process and a final result. In , the authors chose the most frequent final result as the true final result, significantly promoting the accuracy.

The nature of this technique is statistical. We assume that the model is so well trained that the most frequent and stable answer is most likely to be the right one. However, there still exist drawbacks. Naive self-consistency is only concerned about choosing the best final answer, omitting the intermediate results. This can be damaging to interpretability, as the same final result does not imply the same reasoning process. The best pair of reasoning and final answer can be still chosen based on bias or even wrong intermediate steps. Using more complex algorithms such as clustering and human-machine interaction, self-consistent CoT might be further improved, especially in promoting the accuracy of intermediate reasoning.

In summary, CoT and its variants are a representative attempt in LLMs to expose the inference process to the users as much as possible, in a way that humans can interpret. The main problem in CoT is that models except LLMs often fail to generate human-readable intermediate logic fragments, limiting its usage.

Mechanistic Interpretability

While CoT provides evidence of how an LLM makes decisioons, it does not fully reveal the underlying mechanism upon which models are working. Mechanistic interpretability uses knowledge about the mechanisms underlying a network's decision-making to predict its behavior . This is not like designing an interpretable model in the very first place, but requires reverse-engineering to explain how models predict the results, step by step through their internals.

Therefore, mechanistic interpretability assumes (or hopes) that there exists at least one minimal component in the model that we are interested in, which can be interpreted. Once this assumption holds, we reverse-engineer the model, figuring out what these components are doing, respectively. Surely there are a large number of candidate "components" to be researched: from a single neuron, to combinations of neurons (a.k.a. directions) and even layers. Usually the first job is to find that proper, interpretable component. This is a foundamental step, and is often frustrating, partially for the following reasons:

1. There are too many candidates. Apart from the most basic neurons, the combination of neurons, and even the combination of these combinations, can all be candidate components. Sometimes we need to involve more neurons to make sure that the features to be expressed are represented intactly.
2. Candidates face polysemanticity. Even though we hope that each basic component represents only a single feature (or performs a single function), it is often not the truth. Every single activation has the potential to be part of different, unrelated information flows. To solve this problem, either do we disentangle them, or should we design a disentangled model in the first place.
3. Even if we can find proper components, we can't always ensure that they are interpretable. Components that deal with a single feature might be a small part of a larger component. For example, if we train a model to process signals, and fortunately there exist small components, each of which processes signals in different ways, and they together form a large component that performs Fourier transforms. We might still find the smaller components meaningless, because we need to consider them as a whole to realize that they are performing Fourer transforms.

All of these factors makes the analysis of simple models extremely complex. Despite the fact that there are many in pursuit of mechanistic interpretability, I still believe that we need to interpret models more globally and concisely.

Polytopes — Polytobes Used for Mechanistic Interpretability : the authors interpret the piecewise activation functions (such as ReLU) as partitioning the activation space into multiple polytopes, where the inputs are placed. This doesn't fully explain linear models semantically, though.

Attribution-Based Interpretability

References

Quanshi Zhang, Zhu Songchun. "Visual interpretability for deep learning: a survey". Frontiers of Information Techonology & Electrical Engineering 19.1 (2018): 27-39.
Leonida Gianfagna and Antonio Di Cecco. "Explainable AI with Python". Switzerland AG. Part of Springer Nature.
Jason Wei, Xuezhi Wang, et al. "Chain-of-Thought Prompting Elicits Reasoning in Large Language Models". 36th Conference on Neural Information Processing Systems (NeurIPS 2022).
Xuezhi Wang, Jason Wei, et al. "Self-Consistency Improves Chain of Thought Reasoning in Language Models". ICLR 2023.
Lee Sharkey, Bilal Chughtai, et al. "Open Problems in Mechanistic Interpretability". arXiv:2501.16496v1.
Sid Black, Lee Sharkey, et al. "Interpreting Neural Networks through the Polytope Lens". arXiv:2211.12312v1.
Karen Simonyan, Andrea Vedaldi, et al. "Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps". arXiv:1312.6034v2.